To form a solid square out of dominoes, you have to use either 2, 8 or 18 dominoes, as this diagram shows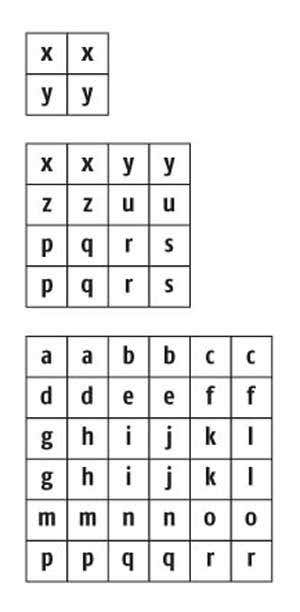
Answer: 0-0 and 2-2
The winner is Philip Mottram of Aura, Finland. There were 97 entries.
Advertisement
Worked answer
The number of dominoes in a standard set is 28. The total number of pips is 168.
The number of dominoes, each twice as long as broad, which can form a solid square is 2, 8, or 18 (see image, right).
There is no way in which I could arrange two dominoes that were not the same to form a chain (for example, 6-6 and 2-2, which do sum to a perfect square, could only form a ring 6-2 2-6).
Therefore my two lots are 8 and 18, and I have still to find two more dominoes. The maximum sum from those two dominoes is 23 (6-6 6-5) and the minimum is 1 (0-0 0-1).
If a closed chain is to be formed, each number must occur either twice, four times or six times, and the sum of the chain must be even.
Perfect even squares are: 4, 16, 36, 64, 100 and 144.
Therefore, the total must lie between 168 – 23 = 145, and 168 – 1 = 167.
144 + 4 = 148 is clearly impossible, so the only possibility is 100 + 64 = 164.
Therefore, I have to have 4 pips on the two dominoes missing. These might be:
- 0-1 and 1-2
- 0-2 and 1-1
- 0-0 and 2-2
Either of the first two will leave an odd number of 0 and 2 in the chain, so the only possibility is 0-0 and 2-2.
It may be helpful to show two of the many possible chains that could be formed:
2-4 4-3 3-3 3-5 5-5 5-4 4-6 6-2 (= 64)
6-0 0-4 4-4 4-1 1-1 1-2 2-5 5-1 1-3 3-2 2-0 0-1 1-6 6-5 5-0 0-3 3-6 6-6 (= 100)


